Chaos in Faust

Voor blok A hebben we het volgende:
a-plus.png

[imath] \mathrm{y}(n) = - (\omega_0)^2 \cdot \mathrm{f}(n) [/imath]

Start regelt het opstarten van de oscillatie, maar dat doen we in onze differentievergelijking via de beginvoorwaarden, zodat we "start" hier verder kunnen weglaten.
 
Laatst gewijzigd:
En nu de zaak aan elkaar plakken:
c-plus.png

[imath] \mathrm{y}(n) = - (\omega_0)^2 \cdot \mathrm{f}(n) [/imath]

[imath] \mathrm{y}(n) = - (\omega_0)^2 \cdot \mathrm{e}(n-1) [/imath]

[imath] \mathrm{y}(n) = - (\omega_0)^2 \cdot \{2 \mathrm{e}(n-2) - \mathrm{e}(n-3) + \mathrm{a}(n-1)/\mathrm{SR}^2 \} [/imath]

[imath] \mathrm{y}(n) = - (\omega_0)^2 \cdot \{2 \mathrm{f}(n-1) - \mathrm{f}(n-2) + \mathrm{y}(n-1)/\mathrm{SR}^2 \} [/imath]

[imath] \mathrm{y}(n) = - (\omega_0)^2 \cdot \{\frac{-2 \mathrm{y}(n-1)}{(\omega_o)^2} + \frac{\mathrm{y}(n-2)}{(\omega_0)^2} + \mathrm{y}(n-1)/\mathrm{SR}^2 \} [/imath]

[imath] \mathrm{y}(n) = 2 \mathrm{y}(n-1) - \mathrm{y}(n-2) - (\frac{\omega_0}{ \mathrm{SR}})^2 \cdot \mathrm{y}(n-1) [/imath]

[imath] \mathrm{y}(n) = \left (2 - (\frac{\omega_0}{ \mathrm{SR}})^2 \right ) \cdot \mathrm{y}(n-1) \, - \, \mathrm{y}(n-2) \,\,\,\,\,\,\,\, (^*) [/imath]
 
En nu is er dus iets gruwelijks fout gegaan! Het Riedeltest progje geeft geen chaotisch signaal, en was enkel maar om te achterhalen of ik de formule voor de Faust integrator juist had. Vandaar dat er ook geen arctangens in de loop zit. Ik heb nu dus de differentievergelijking voor het verkeerde Faust progje uitgerekend. :(:duivels::duivels::duivels::stupid;{=(
 
Laatst gewijzigd:
Goed - mijn innerlijke rust is weer enigszins terug. Elk nadeel heeft zijn voordeel. Dus we kunnen nu in elk geval even controleren of de gevonden differentievergelijking inderdaad dezelfde oplossingen geeft die de online Faust IDE voor Riedeltest opleverde. Riedeltest gaf voor een sample rate SR van 48000 samples/sec periodieke signalen met een hoekfrequentie van ongeveer de [imath] \omega_0 [/imath] uit mijn differentievergelijking. Ben nu op zoek naar een (al dan niet online) programma waarmee ik een stukje van de oplossing van mijn differentievergelijking voor verschillende waarden van [imath] \omega_0 [/imath] kan plotten. Die oplossingen moeten dan als het goed is weer periodieke signalen met omgerekend een hoekfrequentie van ongeveer [imath] \omega_0 [/imath] zijn.
 
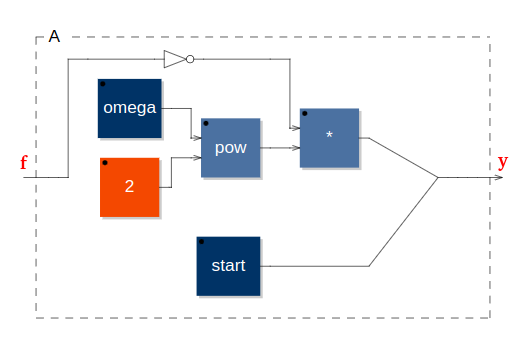
We bekijken de frequenties: f1 = 100 Hz, f2 = 1000 Hz en f3 = 10000 Hz. Die drie gevallen corresponderen met een [imath] \omega_0 [/imath] van respectievelijk:

[imath] 1) \,\,\, \omega_1 = 2 \pi \mathrm{f}_1 = 628.319 \,\, \mathrm{rad}/s [/imath]
[imath] 2) \,\,\, \omega_2 = 2 \pi \mathrm{f}_2 = 6283.19 \,\, \mathrm{rad}/s [/imath]
[imath] 3) \,\,\, \omega_3 = 2 \pi \mathrm{f}_3 = 62831.9 \,\, \mathrm{rad}/s [/imath]

Zodat:

[imath] 1) \,\,\, 2 - \left ( \frac{\omega_1}{\mathrm{SR}} \right )^2 \,\, = \,\, 1.99983 [/imath]
[imath] 2) \,\,\, 2 - \left ( \frac{\omega_2}{\mathrm{SR}} \right )^2 \,\, = \,\, 1.98287 [/imath]
[imath] 3) \,\,\, 2 - \left ( \frac{\omega_3}{\mathrm{SR}} \right )^2 \,\, = \,\, 0.28652 [/imath]

Verder gaan we voor het gemak uit van [imath] \mathrm{y}(0) = 0 [/imath] en [imath] \mathrm{y}(-1) \neq 0 [/imath]. Als oplossingen voor de differentievergelijking (*) voor de gevallen 1), 2) en 3) levert Wolfram Alpha ons dan:

1.png


2.png


3.png


De vraag is nu dus of de frequenties van de bovenstaande drie via de differentievergelijking (*) gegenereerde signalen (naar de tijdschaal omgerekend) net als bij het Riedertest progje ongeveer overeenkomen met f1, f2 en f3? Zo ja - dan werken Faust en de computer zelf waarschijnlijk ook met differentievergelijkingen. Later verder...
 
Had nog even tijd maar ik moet nu toch echt weg. Er lijkt nog steeds iets mis te zijn want de oplossingen geven (deels) complexe getalwaarden voor y(n). Dat kan niet kloppen want als je y(0) en y(-1) als reële beginwaarden opgeeft kun je y(n) met de differentievergelijking (*) ook voor n=1 uitrekenen, en dan voor n=2, dan voor n=3, etc. En dat moeten dan ook steeds weer reële getallen zijn. Alle waarden van y(n) voor n> -2 moeten dus reëel zijn. :stupid

Wie ziet de fout...?
 
Mogelijk raakt Wolfram Alpha in de war als er maar een van de twee beginvoorwaarden gegeven is. Met twee beginvoorwaarden krijgen we:

1-vervolg.png


De twee extreem kleine getallen in het antwoord zijn vermoedelijk afrondingsfouten, laten we die weg dan wordt het:

[imath] \mathrm{y}(n) = 38.3491 \, i \, \cdot \{ (0.999915 - 0.0130381 \, i)^n \,\, - \,\, (0.999915 + 0.0130381 \, i)^n \} [/imath]

[imath] \mathrm{y}(n) = 38.3491 \, i \, \cdot \{ (\cos(0.013038) - i \, \sin(0.013038) )^n \,\, - \,\, (\cos(0.013038) + i \, \sin(0.013038) )^n \} [/imath]

[imath] \mathrm{y}(n) = 38.3491 \, i \, \cdot \{ (\cos(0.013038 \cdot n) - i \, \sin(0.013038 \cdot n) ) \,\, - \,\, (\cos(0.013038 \cdot n) + i \, \sin(0.013038 \cdot n) ) \} [/imath]

[imath] \mathrm{y}(n) = 38.3491 \, i \, \cdot - 2 i \, \sin(0.013038 \cdot n) [/imath]

[imath] \mathrm{y}(n) = 76.698 \cdot \sin(0.013038 \cdot n) [/imath]
 
Voor geval 1) met twee beginvoorwaarden vonden we in het vorige berichtje dat:

[imath] \mathrm{y}(n) = 76.698 \cdot \sin(0.013038 \cdot n) [/imath]

Voor precies een volledige trilling moet het argument [imath] 0.013038 \cdot n [/imath] van de sinus dus [imath] 2 \pi [/imath] doorlopen. Dit vereist N samples waarbij [imath] 0.013038 \cdot \mathrm{N} = 2 \, \pi [/imath]. Dus:

[imath] \mathrm{N} = \frac{ 2 \, \pi}{ 0.013038 } [/imath]

Voor de trillingstijd T van y(n) bij een sample rate SR van 48000 samples/sec vinden we dan:

[imath] \mathrm{T} = \mathrm{N} \cdot \frac{1}{\mathrm{SR}} [/imath]

[imath] \mathrm{T} = \frac{ 2 \, \pi}{ 0.013038 } \cdot \frac{1}{\mathrm{SR}} [/imath]

[imath] \mathrm{T} = \frac{ 2 \, \pi}{ 0.013038 \cdot \mathrm{SR} } [/imath]

Dus de frequentie f van y(n) is:

[imath] f = \frac{ 0.013038 \cdot \mathrm{SR} }{ 2 \, \pi} [/imath]

[imath] f = 99.6 \, \mathrm{Hz} [/imath]

Dat is een heel mooi resultaat dat overeen stemt met mijn bevindingen bij het runnen van het Faust progje! Er zou in principe nog veel meer te controleren zijn, maar hiermee heb ik weer voldoende vertrouwen in mijn aanpak. :)
 
Nu ben ik het volgende van plan:

1. Het eenvoudigste Faust progje zoeken dat "riedelt".
2. De differentievergelijking opstellen van dat Faust progje.
3. Onderzoeken of die differentievergelijking riedel-achtige oplossingen heeft.

En blijkt dat laatste het geval dan kunnen we het riedelen zien als een noodzakelijk gevolg van de implementatie van de betreffende differentievergelijking in het gebruikte Faust progje. Of daar dan wiskundig nog meer over te zeggen valt dat voor het ontwerp van synths bruikbaar is valt nog te bezien. Het kon mij wel eens te ingewikkeld worden...
 
Op basis van onderstaande progje stel ik vast dat hier twee situaties aan de orde zijn:

1. Voor lage gain krijg je een keurige oscillator met een voor toenemende gain toenemende amplitude en frequentie.
2. Op zeker moment gaat dat over in aliasing en/of clipping, en van deze tweede situatie is geen terugkeer naar de eerste meer mogelijk (afgezien van een herstart).

Code: 
declare name "Element";

import("maths.lib");
import("filters.lib");

start  = 0.01*button("start");
gain = hslider("gain",0.01, 0.0001,5,0.000001);


A = _ , start :> _*-1 : _ ;
B = _ : integrator : _*gain : integrator : _*gain : atan : _;
C = A~B ;

safe(x) = atan(x)/3;

process = C <: safe,safe : _,_ ;

(Bij het weglaten van de "atan" in de loop komt de tweede situatie niet meer voor maar loopt het progje in plaats daarvan dan vast met een NaN-melding, waarschijnlijk omdat de getallen dan te groot worden.)
 
Goed - onderstaand progje riedelt na het opstarten uitbundig, dus daar ga ik voor de bepaling van de differentievergelijking van uit:

riedel.png


De kern van de zaak vormt blok C waarbij we het startblok nog kunnen weglaten want dat speelt na het opstarten geen rol meer. Het opstarten zelf wordt door de beginvoorwaarden van de differentievergelijking weergegeven.
 
Hier gaat het dus om:
riedel-kern.png


(Waarbij ik het als parameter hier gekozen getal 1000000000 verder voor het gemak als g zal aangeven.)
 
Voor de twee integrators achter elkaar hebben we:

[imath] s_1 : integrator_1 : s_2 : integrator_2 : s_3 [/imath]

met:

[imath] s_2(n) = s_1(n) + s_2(n-1) [/imath]
[imath] s_3(n) = s_2(n) + s_3(n-1) [/imath]

Dus:

[imath] s_3(n) = s_1(n) + s_2(n-1) + s_3(n-1) [/imath]

[imath] s_3(n) = s_1(n) + s_3(n-1) - s_3(n-2) + s_3(n-1) [/imath]

[imath] s_3(n) = s_1(n) + 2 \, s_3(n-1) - s_3(n-2) [/imath]
 
riedelen.png

We hebben nu:

[imath] z(n) = \arctan(y(n)) + 2 \, z(n-1) - z(n-2) [/imath]
[imath] y(n) = -\mathrm{g} \, z(n-1) [/imath]

Anders geschreven:

[imath] z(n) - 2 \, z(n-1) + z(n-2) = \arctan(y(n)) [/imath]
[imath] z(n) = - \frac{1}{\mathrm{g}} y(n+1) [/imath]

En dus:

[imath] - \frac{1}{\mathrm{g}} y(n+1) \,\, + \,\, 2 \, \frac{1}{\mathrm{g}} y(n) \,\, - \,\, \frac{1}{\mathrm{g}} y(n-1) = \arctan(y(n)) [/imath]

[imath] y(n+1) \,\, - \,\, 2 \, y(n) \,\, + \,\, y(n-1) = - \mathrm{g} \, \arctan(y(n)) [/imath]

[imath] y(n) \,\, - \,\, 2 \, y(n-1) \,\, + \,\, y(n-2) = - \mathrm{g} \, \arctan(y(n-1)) [/imath]
 
[imath] y(n) \,\, - \,\, 2 \, y(n-1) \,\, + \,\, y(n-2) = - \mathrm{g} \, \arctan(y(n-1)) [/imath]

Dit is 'm dus. Net even in Wolfram Alpha geprobeerd, maar die komt er niet uit. Op zoek naar een ander programma dus om te zien hoe de getallenrij y(n) als functie van n eruit ziet. En dat voor verschillende beginvoorwaarden.
 
Is weer even geleden dat ik met Python bezig was. Eerst maar even uitproberen met een onzin-rijtje:

Code: 
import numpy as np
import matplotlib.pyplot as plt
x0 = 1 # eerste beginvoorwaarde
x1 = 2 # tweede beginvoorwaarde
g = 0.7 # gain-parameter
N = 4 # aantal afgebeelde punten
index_set = range(N+1)
x = np.zeros(len(index_set))
x[0] = x0
x[1] = x1
for n in index_set[1:]:
  x[n] = x[n-1] + x[n-2]
plt.plot(index_set, x, 'ro')
plt.xlabel('argument n')
plt.ylabel('functiewaarde y(n)')
plt.show()

Dat geeft deze plot:

plot.png


- Klopt dat?
 
Hm - het voorbeeld-rijtje is minder onzinnig dan ik dacht. Zie: Rij van Fibonacci - Wikipedia

Neemt niet weg dat er nog iets mis is, want 1 en 2 staan in het plotje als functiewaarden voor n=1 en n=2 in plaats van voor n=0 en n=1 (zoals ik in het progje als beginvoorwaarden had opgegeven).
 
Je dient in te loggen of je te registreren om een bericht te kunnen plaatsen.

Vergelijkbare discussies

T
  • Gesloten
ATC Pro scm 50asl
Reacties
2
Bekeken
2K
Tubbes85
T
ontwerper
  • Gesloten
SSL AlphaLink Madi AX, MadiXtreme 64 en Duende Native plugin studio bundle
Reacties
11
Bekeken
4K
ontwerper
ontwerper
S
  • Gesloten
BugBrand PEQ V2 (2014) Parametric Equaliser
Reacties
1
Bekeken
2K
Spindrift
S
glowingfish
  • Gesloten
Roland SRV2000 en Peavy addverb 3
Reacties
6
Bekeken
2K
glowingfish
glowingfish
Alvarius
  • Gesloten
MOOG THREE BAND PARAMETRIC EQUALIZER
Reacties
3
Bekeken
1K
Alvarius
Alvarius
Back
Top